Quaternions with C++ implementation

Full C++ implementation of Quaternions here
To understand quaternions, you first need to understand vectors and matrices, especially matrices because quaternions complement matrices by solving problems that arise when using matrices to represent rotations.
Don’t get me wrong: matrices are awesome. They work great for most transformations like rotations and translations especially in 2D and 3D scenarios like physics simulations, computer graphics, or games. But when it comes to smooth interpolation and using euler angles matrices have their down sides.
Okay let’s rewind and revisit the basics vectors, matrices, and how we rotate things to understand better 🙂
A vector like (2, 3, 4) represents a point in 3D space. This just means:
- 2 units along the X-axis,
- 3 units along the Y-axis,
- 4 units along the Z-axis.
To rotate a point in 3D space, we usually build individual rotation matrices for the X, Y, and Z axes, then combine them through matrix multiplication.
Each axis has its own rotation matrix (shown here for a generic angle θ):
┌ ┐ ┌ ┐ ┌ ┐
Rx = │ 1 0 0 │ Ry = │ cos θ 0 sin θ │ Rz = │ cos θ -sin θ 0 │
│ 0 cos θ -sin θ│ │ 0 1 0 │ │ sin θ cos θ 0 │
│ 0 sin θ cos θ│ │-sin θ 0 cos θ │ │ 0 0 1 │
└ ┘ └ ┘ └ ┘
To apply a full 3D rotation, we compose these matrices (in a specific order):
Rotation Matrix =Rz(θ) ⋅ Ry(θ) ⋅ Rx(θ)
Vrotated= Rotation Matrix ⋅ V
Where V is your original 3D vector (or set of vectors, like a cube).
To model a cube in 3D, you define its 8 corner points (vertices), like this:
cube = [
[-1, -1, -1],
[-1, -1, 1],
[-1, 1, -1],
[-1, 1, 1],
[ 1, -1, -1],
[ 1, -1, 1],
[ 1, 1, -1],
[ 1, 1, 1]
]
This is an 8×3 matrix (or 3×8 if you treat it column-wise). Each row is a vector representing a cube corner in 3D space.
You rotate all the points with:
rotated_cube = cube ⋅ RotationMatrixᵀ
You can visualize this as in the gif below:
But manually building these 3 rotation matrices each time is tedious and error-prone, and also order matters since matrix multiplication is not commutative: A * B ≠ B * A. Even small mistakes in order or axis orientation can completely mess up your transformation
To make representation easier, we often use Euler angles, which are just 3 values (pitch, yaw, roll) representing rotation around the X, Y, and Z axes.These angles are intuitive and human-friendly but under the hood, they’re still converted into rotation matrices using the exact same formulas shown earlier. Euler angles are just a compact input format; the math remains the same.
Euler(30°, 45°, 0°)
This means:
Rotate 30° around the X-axis (pitch),
then 45° around the Y-axis (yaw),
then 0° around the Z-axis (roll).
While Euler angles are great for describing rotations around the standard X, Y, and Z axes, they fall short when you need to spin around an arbitrary direction say, diagonally between X and Y.
That’s where axis-angle rotation comes in.
Instead of doing three separate rotations like Euler (X → Y → Z), axis-angle lets you rotate once around a custom axis in space. It's more flexible and intuitive when you're not constrained to the world axes.
It’s like saying:
“Rotate 60° around the direction pointing toward (1, 1, 0)” a diagonal between the X and Y axes.
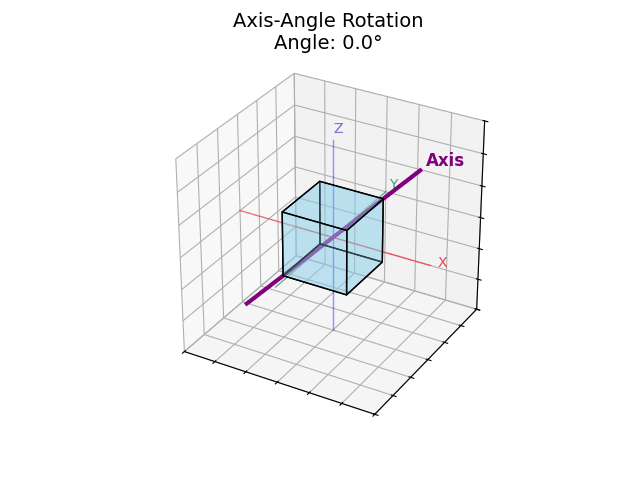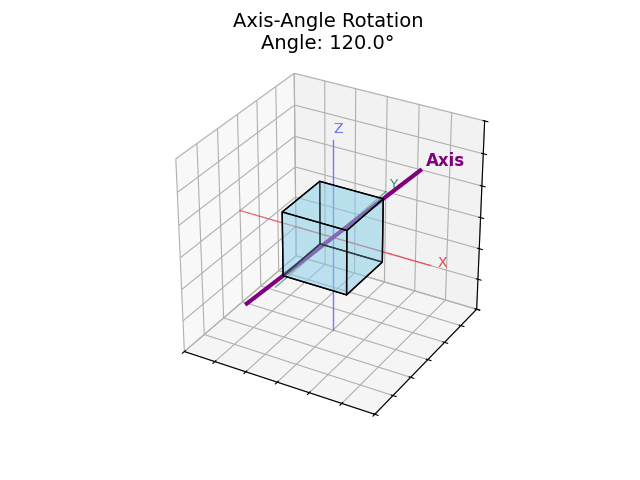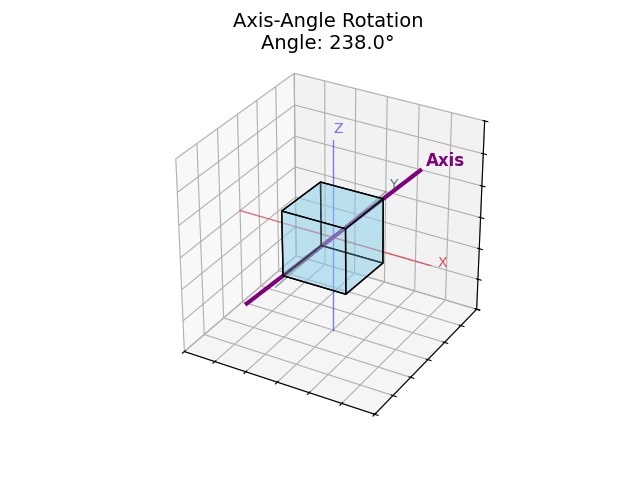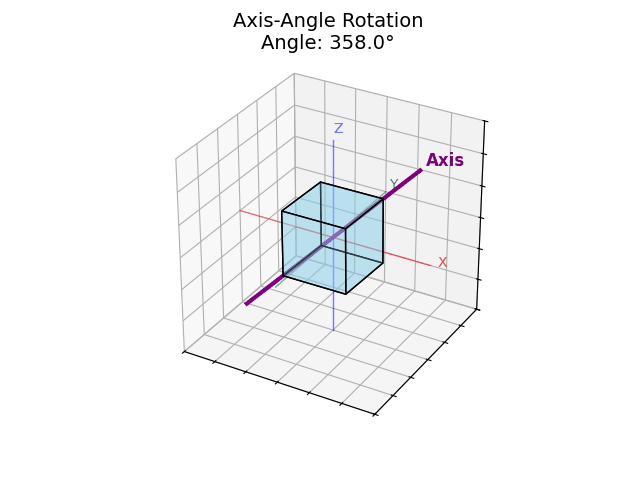
Axis: (1, 1, 0) → Normalized to (0.707, 0.707, 0)
Angle: 60°
This means: rotate the object 60° around the axis pointing diagonally between X and Y.
Axis-angle gives you more control, and it's especially useful for visualizing things like spinning tops or tilting cameras.
Okay enough of matrixes, if they are so great why then do we need quaternions and what even are quaternions
Quaternions are a mathematical way of representing rotation in 3D space just like Euler angles and rotation matrices but they do it more robustly (more on than soon). They solve two big problems: gimbal lock and smooth interpolation.
- Gimbal Lock: This is a common issue with Euler angles. Gimbal lock happens when two of the three rotation axes become aligned, which collapses a degree of freedom. This only occurs in Euler because the rotations are applied one axis at a time, in sequence.
check out these videos to see Gimbal lock animation:
Euler vs Quaternion - What's the difference?
You might ask:
“Why not just use axis-angle rotation with matrices then? Problem solved.”
And sure, axis-angle avoids gimbal lock in theory. But it runs into its own issues which is the second big problem:
- Smooth Interpolation: Let’s say your object is facing direction A, and you want to rotate it smoothly to direction B like a spaceship turning or a character looking around. Interpolating using Euler representation can lead to weird artifacts like wobbling, stuttering, or nonlinear motion because each axis is interpolated independently, which doesn't guarantee a natural path. Even axis-angle interpolation can behave oddly, especially when the start and end axes are very different.
Quaternions, on the other hand, represent rotations as points on a 4D sphere. So instead of interpolating in a straight line through space, quaternions use something called SLERP (Spherical Linear Interpolation), it travels along the shortest arc on the sphere like following the curve of the rotation, not cutting through it.
It’s smoother, more natural, and avoids all those blending issues.
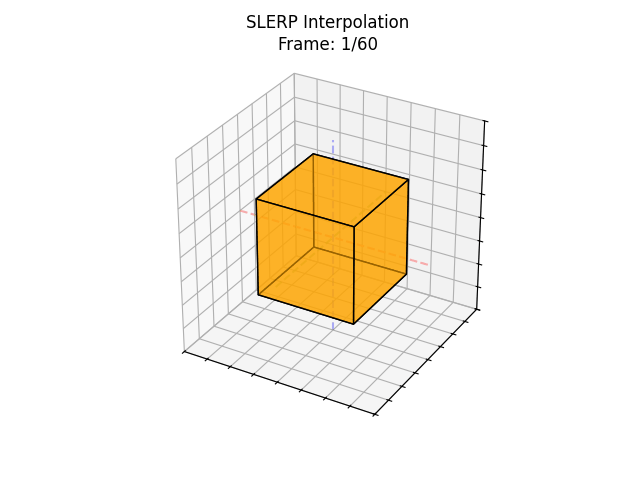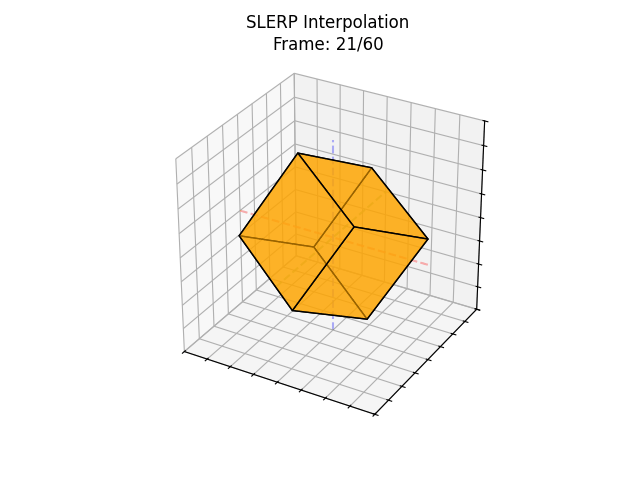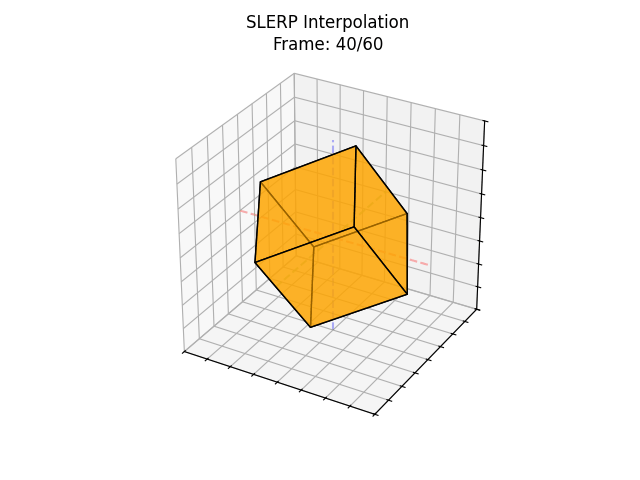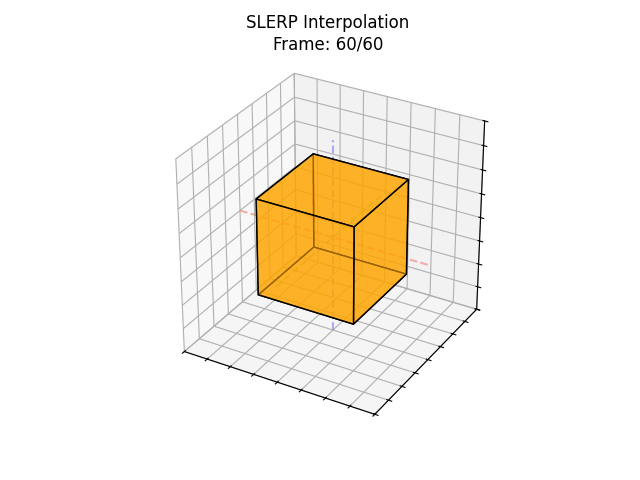
So... what is a Quaternion?
You can think of a quaternion as a special 4D number that encodes both the axis and the angle of rotation all in one neat package. It’s kind of like axis-angle, but with math that’s better suited for combining and interpolating rotations.
It looks like this:
q = [w, xi, yj, zk]
Where:
- (x, y, z) is a unit vector pointing along the axis of rotation
- w is the cosine of half the rotation angle
- And i, j, k are imaginary units, similar to complex numbers with some rules:
i² = j² = k² = ijk = -1
i × j = k, j × k = i, k × i = j (but order matters!)
Yes, it’s mathy. But the point is: all of this lets us rotate objects in 3D space without suffering from the common problems of gimbal lock or odd blending.
Jeremiah's blog on Understanding Quaternions does an excellent job in explaining the maths behind it .
Let's say you want to rotate an object 90° around the axis pointing diagonally up and to the right: (1, 1, 1).
Step 1: Normalize the axis
axis = (1, 1, 1)
normalized_axis = (1, 1, 1) / √(1² + 1² + 1²) = (0.577, 0.577, 0.577)
Step 2: Create the quaternion For a 90° rotation, we use half the angle (45°):
w = cos(45°) = 0.707
x = 0.577 × sin(45°) = 0.577 × 0.707 = 0.408
y = 0.577 × sin(45°) = 0.577 × 0.707 = 0.408
z = 0.577 × sin(45°) = 0.577 × 0.707 = 0.408
So our quaternion is: q = [0.707, 0.408i, 0.408j, 0.408k]
Step 3: Apply it to a point Let's rotate the point (1, 0, 0):
- Original point: (1, 0, 0)
- After 90° rotation around (1,1,1): approximately (0.333, 0.667, 0.667)
Thing is, whether you use Euler, axis angle or Quaternions you will get same answer only that they don't all get there the same way. And they don’t all behave well when you try to combine or interpolate rotations.
Here’s the beauty: quaternions aren’t locked in a vacuum. You can convert back and forth between Euler, axis-angle, and quaternions depending on what you need and what you need depends on what you are doing.
So when do you use what?
- Euler angles are great when you're working with something familiar like pitch/yaw/roll or when your user interface expects intuitive angles. They're easy to read, but can suffer from gimbal lock and awkward interpolation.
- Axis-angle is useful when you know you want to rotate around a specific direction by a specific amount. it's concise and geometrically meaningful. But interpolation between two axis-angle rotations isn't always smooth too.
- Quaternions are ideal for:
- Smooth, continuous rotation (no weird stuttering)
- Avoiding gimbal lock entirely
- Interpolating between rotations using SLERP
- Storing and composing rotations compactly and efficiently
Conversion is always possible:
Euler → Quaternion
Quaternion → Euler
Axis-Angle → Quaternion
Quaternion → Axis-Angle
Quaternion → Rotation Matrix (for applying transforms)
Rotation Matrix → Quaternion (to extract orientation)
So you're never stuck. Pick the format that’s easiest for your current task and convert when needed 🙂.